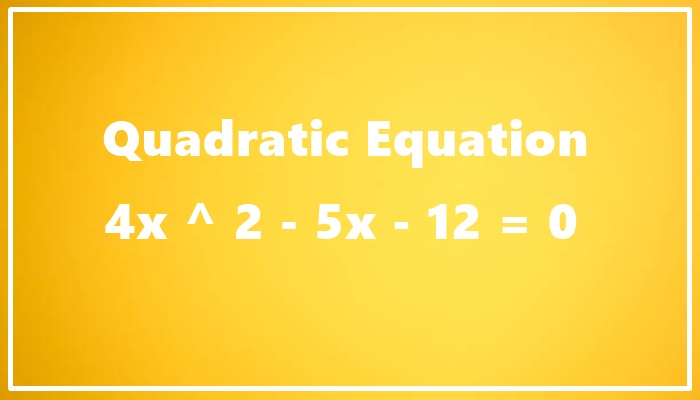Quadratic equations are a fundamental aspect of algebra and often appear in various mathematical problems. In this blog, we will explore the solution to the quadratic equation 4×2−5x−12=04x^2 – 5x – 12 = 04×2−5x−12=0, covering methods to solve it and interpreting the results.
Understanding Quadratic Equations
A quadratic equation is a second-degree polynomial equation in the form of ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0, where aaa, bbb, and ccc are constants. In our equation, a=4a = 4a=4, b=−5b = -5b=−5, and c=−12c = -12c=−12. The solutions to this equation are the values of xxx that make the equation true.
Methods to Solve the Quadratic Equation
There are several methods to solve quadratic equations, including factoring, using the quadratic formula, and completing the square. In this blog, we will focus on solving the equation 4×2−5x−12=04x^2 – 5x – 12 = 04×2−5x−12=0 using the quadratic formula.
The Quadratic Formula
The quadratic formula is a universal method to solve any quadratic equation. It is given by:
x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}x=2a−b±b2−4ac
This formula provides two solutions, one for the positive root (+++) and one for the negative root (−-−).
Applying the Quadratic Formula
To solve 4×2−5x−12=04x^2 – 5x – 12 = 04×2−5x−12=0, we first identify the values of aaa, bbb, and ccc:
- a=4a = 4a=4
- b=−5b = -5b=−5
- c=−12c = -12c=−12
Substituting these values into the quadratic formula, we get:
x=−(−5)±(−5)2−4⋅4⋅(−12)2⋅4x = \frac{-(-5) \pm \sqrt{(-5)^2 – 4 \cdot 4 \cdot (-12)}}{2 \cdot 4}x=2⋅4−(−5)±(−5)2−4⋅4⋅(−12)
Simplifying this, we have:
x=5±25+1928x = \frac{5 \pm \sqrt{25 + 192}}{8}x=85±25+192 x=5±2178x = \frac{5 \pm \sqrt{217}}{8}x=85±217
Therefore, the solutions are:
x1=5+2178x_1 = \frac{5 + \sqrt{217}}{8}x1=85+217 x2=5−2178x_2 = \frac{5 – \sqrt{217}}{8}x2=85−217
Interpreting the Solutions
The solutions to the quadratic equation 4×2−5x−12=04x^2 – 5x – 12 = 04×2−5x−12=0 are the values of xxx that satisfy the equation. These solutions can be approximated as:
x1≈2.12x_1 \approx 2.12×1≈2.12 x2≈−1.37x_2 \approx -1.37×2≈−1.37
These roots represent the points where the quadratic function intersects the x-axis.
Graphical Representation
Graphing the quadratic function 4×2−5x−124x^2 – 5x – 124×2−5x−12 can provide a visual understanding of the solutions. The parabola will intersect the x-axis at the points corresponding to x1x_1x1 and x2x_2x2. The vertex of the parabola, the maximum or minimum point, can also be determined using the formula:
x=−b2ax = -\frac{b}{2a}x=−2ab
For our equation, this is:
x=−−52⋅4=58x = -\frac{-5}{2 \cdot 4} = \frac{5}{8}x=−2⋅4−5=85
Substituting x=58x = \frac{5}{8}x=85 back into the equation to find the y-coordinate of the vertex:
y=4(58)2−5(58)−12y = 4 \left(\frac{5}{8}\right)^2 – 5 \left(\frac{5}{8}\right) – 12y=4(85)2−5(85)−12 y=4(2564)−258−12y = 4 \left(\frac{25}{64}\right) – \frac{25}{8} – 12y=4(6425)−825−12 y=10064−20064−76864y = \frac{100}{64} – \frac{200}{64} – \frac{768}{64}y=64100−64200−64768 y=100−200−76864=−86864=−13.56y = \frac{100 – 200 – 768}{64} = \frac{-868}{64} = -13.56y=64100−200−768=64−868=−13.56
So, the vertex of the parabola is at (58,−13.56)\left(\frac{5}{8}, -13.56\right)(85,−13.56).
Conclusion
Solving the quadratic equation 4×2−5x−12=04x^2 – 5x – 12 = 04×2−5x−12=0 using the quadratic formula provides us with the solutions x1=5+2178x_1 = \frac{5 + \sqrt{217}}{8}x1=85+217 and x2=5−2178x_2 = \frac{5 – \sqrt{217}}{8}x2=85−217. These solutions help us understand where the quadratic function intersects the x-axis. Understanding and solving quadratic equations is a crucial skill in mathematics, providing the foundation for more advanced topics.
FAQs
Q1: What is a quadratic equation?
A1: A quadratic equation is a second-degree polynomial equation in the form of ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0.
Q2: What is the quadratic formula?
A2: The quadratic formula is x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}x=2a−b±b2−4ac, used to solve quadratic equations.
Q3: How do you find the vertex of a parabola?
A3: The vertex can be found using x=−b2ax = -\frac{b}{2a}x=−2ab and substituting this xxx value back into the quadratic equation to find the y-coordinate.
Q4: What are the solutions to 4×2−5x−12=04x^2 – 5x – 12 = 04×2−5x−12=0?
A4: The solutions are x1=5+2178x_1 = \frac{5 + \sqrt{217}}{8}x1=85+217 and x2=5−2178x_2 = \frac{5 – \sqrt{217}}{8}x2=85−217.